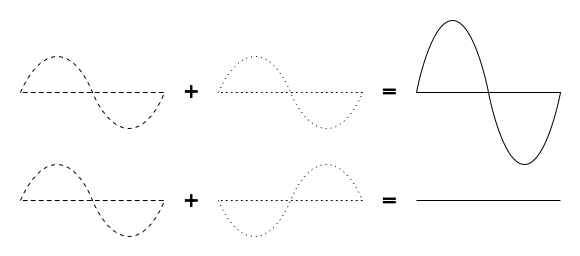|
Dimensione: 37736
Commento:
|
Dimensione: 38041
Commento: converted to 1.6 markup
|
| Le cancellazioni sono segnalate in questo modo. | Le aggiunte sono segnalate in questo modo. |
| Linea 8: | Linea 8: |
| [[TableOfContents]] | <<TableOfContents>> |
| Linea 15: | Linea 15: |
| Ma come fate a sapere dove stanno andando le onde radio emesse dalla vostra interfaccia di rete wireless? Cose succede quando queste onde rimbalzano contro gli oggetti nella vostra stanza o contro gli altri palazzi in un collegamento all’esterno? Come possono essere usate diverse schede di rete wireless nella stessa area senza interferire l’una con l’altra? | Ma come fate a sapere dove stanno andando le onde radio emesse dalla vostra interfaccia di rete wireless? Cosa succede quando queste onde rimbalzano contro gli oggetti nella vostra stanza o contro gli altri palazzi in un collegamento all’esterno? Come possono essere usate diverse schede di rete wireless nella stessa area senza interferire l’una con l’altra? |
| Linea 21: | Linea 21: |
| Tutti conosciamo le vibrazioni o oscillazioni in diverse forme: un pendolo, un’albero che ondeggia al vento, la corda di una chitarra – sono tutti esempi di oscillazioni. | Tutti conosciamo le vibrazioni o oscillazioni in diverse forme: un pendolo, un albero che ondeggia al vento, la corda di una chitarra – sono tutti esempi di oscillazioni. |
| Linea 42: | Linea 42: |
| Le onde hanno anche una proprietà chiamata ampiezza. E’ la distanza tra il centro dell’onda all’estremità di uno dei suoi picchi, si può immaginarla come l’altezza di un’onda nell’acqua. La relazione tra la frequenza, la lunghezza d’onda, e l’ampiezza è mostrata nella Figura 2.1. | Le onde hanno anche una proprietà chiamata ampiezza. È la distanza tra il centro dell’onda all’estremità di uno dei suoi picchi, si può immaginarla come l’altezza di un’onda nell’acqua. La relazione tra la frequenza, la lunghezza d’onda, e l’ampiezza è mostrata nella Figura 2.1. |
| Linea 48: | Linea 48: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.1.png|| | ||<:>{{attachment:figure-2.1-ita.png}}|| |
| Linea 108: | Linea 108: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.2.png|| | ||<:>{{attachment:figure-2.2-ita.png}}|| |
| Linea 125: | Linea 125: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.3.png|| | ||<:>{{attachment:figure-2.3-ita.png}}|| |
| Linea 140: | Linea 140: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.4.png|| | ||<:>{{attachment:figure-2.4-ita.png}}|| |
| Linea 202: | Linea 202: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.5.png|| | ||<:>{{attachment:figure-2.5.png}}|| |
| Linea 217: | Linea 217: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.6.png|| | ||<:>{{attachment:figure-2.6-ita.png}}|| |
| Linea 222: | Linea 222: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.7.png|| | ||<:>{{attachment:figure-2.7-ita.png}}|| |
| Linea 227: | Linea 227: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.8.png|| | ||<:>{{attachment:figure-2.8.png}}|| |
| Linea 236: | Linea 236: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.9.png|| | ||<:>{{attachment:figure-2.9.png}}|| |
| Linea 263: | Linea 263: |
| ||<:>http://wiki.wndw.net/images/figures/en/figure-2.10.png|| | ||<:>{{attachment:figure-2.10-ita.png}}|| |
| Linea 296: | Linea 296: |
| Any electromagnetic wave carries energy, or power - we can feel that when we enjoy (or suffer from) the warmth of the sun. The power '''P''' is of key importance for making wireless links work: you need a certain minimum power in order for a receiver to make sense of the signal. We will come back to details of transmission power, losses, gains and radio sensitivity in chapter three. Here we will briefly discuss how the power P is defined and measured. The electric field is measured in V/m (potential difference per meter), the power contained within it is proportional to the square of the electric field |
Ogni onda elettromagnetica porta con se energia, o potenza - possiamo rendercene conto quando godiamo (o patiamo) il calore del sole. La potenza '''P''' risulta di importanza fondamentale per il funzionamento dei collegamenti wireless: abbiamo bisogno di una certa potenza minima per far si che un ricevitore riesca a captare un segnale. Ci occuperemo ancora, con più dettagli, di potenza di trasmissione, perdita, guadagno e sensibilità radio nel capitolo tre. In questo capitolo discuteremo brevemente il come la potenza P è definita e misurata. Il campo elettrico è misurato in V/m (differenza di potenziale per metro), la potenza contenuta in esso è proporzionale al quadrato del campo elettrico |
| Linea 306: | Linea 306: |
| Practically, we measure the power by means of some form of receiver, e.g. an antenna and a voltmeter, power meter, oscilloscope, or even a radio card and laptop. Looking at the signal's power directly means looking at the square of the signal in Volts. === Calculating with dBs === By far the most important technique when calculating power is calculating with '''''decibels''''' ('''''dB'''''). There is no new physics hidden in this - it is just a convenient method which makes calculations a lot simpler. The decibel is a dimensionless unit, that is, it defines a relationship between two measurements of power. It is defined by: |
In pratica, la potenza è misurata attraverso un qualche tipo di ricevitore come, ad esempio, un'antenna ed un voltimetro, un power meter, un oscilloscopio o anche una scheda radio ed un computer portatile. Misurare direttamente la potenza di un segnale significa misurare il segnale in Volt al quadrato. === Calcolare con i dB === La tecnica di gran lunga più importante utilizzata per calcolare la potenza è calcolare con i '''''decibels''''' ('''''dB'''''). Non si tratta di un'altra grandezza fisica, è solo un metodo conveniente per rendere i calcoli molto più semplici. Il decibel è un'unità adimensionale, che definisce una relazione tra due misure di potenza. E' definita come: |
| Linea 318: | Linea 318: |
| where '''P1''' and '''P0''' can be whatever two values you want to compare. Typically, in our case, this will be some amount of power. Why are decibels so handy to use? Many phenomena in nature happen to behave in a way we call exponential. For example, the human ear senses a sound to be twice as loud as another one if it has ten times the physical signal. Another example, quite close to our field of interest, is absorption. Suppose a wall is in the path of our wireless link, and each meter of wall takes away half of the available signal. The result would be: {{{ 0 meters = 1 (full signal) 1 meter = 1/2 2 meters=1/4 3 meters=1/8 4 meters=1/16 n meters=1/2^n = 2^-n }}} This is exponential behaviour. But once we have used the trick of applying the logarithm (log), things become a lot easier: instead of taking a value to the n-th power, we just multiply by n. Instead of multiplying values, we just add. Here are some commonly used values that are important to remember: {{{ +3 dB = double power -3 dB = half the power +10 dB = order of magnitude (10 times power) -10 dB = one tenth power }}} In addition to dimensionless dBs, there are a number of relative definitions that are based on a certain base value P0. The most relevant ones for us are: {{{ dBm relative to P0 = 1 mW dBi relative to an ideal isotropic antenna }}} An '''''isotropic antenna''''' is a hypothetical antenna that evenly distributes power in all directions. It is approximated by a dipole, but a perfect isotropic antenna cannot be built in reality. The isotropic model is useful for describing the relative power gain of a real world antenna. Another common (although less convenient) convention for expressing power is in '''''milliwatts'''''. Here are equivalent power levels expressed in milliwatts and dBm: |
dove '''P1''' e '''P0''' possono essere due valori qualsiasi che vogliamo comparare. Tipicamente, nel nostro caso, questi saranno due valori di potenza. Perchè i decibel sono così pratici da usare? Molti fenomeni in natura avvengono con un comportamento che possiamo chiamare esponenziale. Per l'orecchio umano, ad esempio, un suono viene percepito con un volume doppio rispetto ad un altro se possiede dieci volte il suo segnale fisico. Un altro esempio, più vicino al nostro campo di interesse, è l'assorbimento. Supponiamo che sul percorso del nostro collegamento wireless ci sia un muro, e che ogni metro di muro porti via la metà del segnale disponibile. Il risultato sarà: {{{ 0 metri = 1 (segnale pieno) 1 metro = 1/2 2 metri =1/4 3 metri =1/8 4 metri =1/16 n metri =1/2^n = 2^-n }}} Questo è un comportamento esponenziale. Utilizzando il trucco di applicare i logaritmi (log), le cose diventano molto più semplici: invece di elevare un valore alla n-esima potenza, lo moltiplichiamo per n. Invece di moltiplicare i valori li addizioniamo semplicemente. Ecco alcuni valori utilizzati comunemente che è importante ricordare: {{{ +3 dB = il doppio della potenza -3 dB = la metà della potenza +10 dB = ordine di grandezza (10 volte la potenza) -10 dB = un decimo della potenza }}} Oltre i dB adimensionali, vi sono una serie di definizioni relative che fanno riferimento ad un certo valore base P0. Le più importanti per noi sono: {{{ dBm relativo a P0 = 1 mW dBi relativo ad un'antenna isotropica ideale }}} Un' '''''antenna isotropica''''' è un'antenna ipotetiche che distribuisce potenza uniformemente in tutte le direzioni. Normalmente si usa approssimarla con un dipolo ma, in realtà, un'antenna isotropica perfetta non può essere costruita. Il modello isotropico è utile per definire il guadagno relativo in potenza delle antenne del mondo reale. Un'altra convenzione comune (anche se meno conveniente) per esprimere la potenza è il '''''milliwatt'''''. Ecco alcune equivalenze tra potenze in milliwatt e dBm: |
| Linea 364: | Linea 364: |
| == Physics in the real world == Don't worry if the concepts in this chapter seem challenging. Understanding how radio waves propagate and interact with the environment is a complex field of study in itself. Most people find it difficult to understand phenomenon that they can't even see with their own eyes. By now you should understand that radio waves don't travel in a straight, predictable path. To make reliable communication networks, you will need to be able to calculate how much power is needed to cross a given distance, and predict how the waves will travel along the way. There is much more to learn about radio physics than we have room for here. For more information about this evolving field, see the resources list in Appendix A. Now that you have an idea of how to predict how radio waves will interact in the real world, you are ready to start using them for communications. |
== La fisica nel mondo reale == Non è da preoccuparsi se i concetti espressi in questo capitolo sembrano difficili. Capire come le onde radio si propagano e interagiscono con l'ambiente è un campo di studi complesso di per sé. La maggior parte delle persone trova difficile comprendere fenomeni che non possono nemmeno vedere con i propri occhi. Ma ormai abbiamo appreso che le onde radio non viaggiano seguendo un percorso dritto e prevedibile. Per costruire reti di comunicazione affidabili dobbiamo essere in grado di calcolare quanta potenza è richiesta per attraversare una certa distanza, e prevedere come le onde si muoveranno lungo il percorso. C'è ancora molto da imparare sulle onde radio rispetto a quanto si è potuto esporre in questo capitolo per motivi di spazio. Per maggiori informazioni su questo campo in evoluzione vedi le risorse elencate nell'Appendice A. Ora che abbiamo un'idea di come le onde radio si comportano nel mondo reale, siamo pronti per utilizzarle per le nostre comunicazioni. |
Indice
Un’introduzione pratica alla fisica delle onde radio
Le comunicazioni wireless fanno uso di onde elettromagnetiche per inviare segnali attraverso lunghe distanze. Dal punto di vista dell’utente, le connessioni wireless non sono particolarmente differenti da ogni altro tipo di connessione di rete: il web browser, le email e le altre applicazioni lavorano così come ci si aspetta. Ma le onde radio hanno alcune inaspettate proprietà rispetto ai cavi Ethernet. Per esempio, è molto facile vedere il percorso che segue un cavo Ethernet: trovate il connettore che esce dal vostro computer, seguite il cavo fino all’altro capo e lo avrete trovato! Potete anche star certi che stendere molti cavi Ethernet l’uno vicino all’altro non causerà problemi dato che i cavi contengono effettivamente i segnali all’interno del cavo stesso.
Ma come fate a sapere dove stanno andando le onde radio emesse dalla vostra interfaccia di rete wireless? Cosa succede quando queste onde rimbalzano contro gli oggetti nella vostra stanza o contro gli altri palazzi in un collegamento all’esterno? Come possono essere usate diverse schede di rete wireless nella stessa area senza interferire l’una con l’altra?
Per costruire collegamenti wireless stabili e ad alta velocità, è importante comprendere come si comportano le onde radio nel mondo reale.
Cos’è un’onda radio?
Tutti conosciamo le vibrazioni o oscillazioni in diverse forme: un pendolo, un albero che ondeggia al vento, la corda di una chitarra – sono tutti esempi di oscillazioni. Quel che hanno in comune è che a volte, qualche strumento o oggetto, oscilla in modo periodico, con un certo numero di cicli per unità di tempo. Questo tipo di onde sono chiamate a volte onde meccaniche, dato che sono definite dal moto di un oggetto o il suo mezzo di propagazione.
Quando queste oscillazioni viaggiano (è proprio così, l’oscillazione non rimane confinata in un posto) parliamo di onde in propagazione nello spazio. Per esempio, un cantante che canta emette oscillazioni periodiche dalle sue corde vocali. Queste oscillazioni comprimono e decomprimono periodicamente l’aria, e questa variazione periodica della pressione dell’aria lascia la bocca del cantante e viaggia, alla velocità del suono. Una pietra che cade in un lago crea un’increspatura, che attraversa il lago come un’onda.
Un’onda possiede una certa velocità, frequenza e lunghezza d’onda. Questi parametri sono legati da una semplice relazione:
Velocità = Frequenza * Lunghezza d’onda
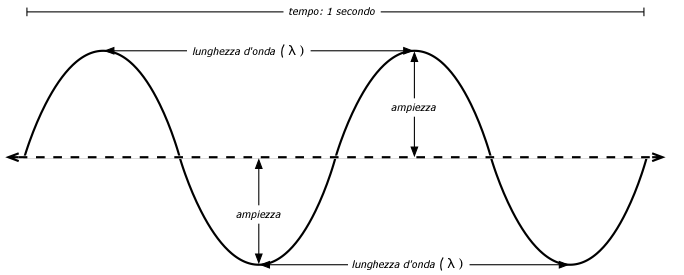
La lunghezza d’onda (a volte chiamata lambda, λ) è la distanza misurata da un punto dell’onda al punto equivalente dell’onda successiva, ad esempio da uno dei picchi fino al prossimo. La frequenza è il numero di onde intere che attraversano un punto fisso in un dato arco di tempo. La velocità è misurata in metri/secondo, la frequenza è misurata in cicli al secondo (o Hertz, abbreviato Hz) e la lunghezza d’onda è misurata in metri.
Ad esempio, se un’onda sull’acqua viaggia ad un metro al secondo, e oscilla cinque volte al secondo, allora ogni onda sarà lunga venti centimetri:
1 metro/secondo = 5 cicli/secondo * W W = 1 / 5 metri W = 0.2 metri = 20 cm
Le onde hanno anche una proprietà chiamata ampiezza. È la distanza tra il centro dell’onda all’estremità di uno dei suoi picchi, si può immaginarla come l’altezza di un’onda nell’acqua. La relazione tra la frequenza, la lunghezza d’onda, e l’ampiezza è mostrata nella Figura 2.1.
Le onde nell’acqua sono semplici da visualizzare. Lasciate cadere semplicemente una pietra nel lago e potrete vedere le onde muoversi attraverso l’acqua in un dato tempo. Nel caso di onde elettromagnetiche, la parte che può risultare più difficile da capire è: “cos’è che oscilla?”
Per comprendere questo, abbiamo bisogno di comprendere le forze elettromagnetiche.
|
Figura 2.1: Lunghezza d’onda, ampiezza e frequenza. Per quest’onda la frequenza è di 2 cicli per secondo, o 2 Hz. |
Forze elettromagnetiche
Le forze elettromagnetiche sono le forze tra cariche elettriche e correnti. Il nostro contatto più diretto con queste è quando la nostra mano tocca la maniglia di una porta dopo aver camminato su un tappeto sintetico, o ![]() strisciare contro un recinto elettrico
strisciare contro un recinto elettrico ![]() . Un esempio più evidente delle forze elettromagnetiche sono i fulmini che possiamo vedere durante i temporali. Le forze elettriche sono le forze che si esercitano tra cariche elettriche. Le forze magnetiche sono le forze che si esercitano tra correnti elettriche.
. Un esempio più evidente delle forze elettromagnetiche sono i fulmini che possiamo vedere durante i temporali. Le forze elettriche sono le forze che si esercitano tra cariche elettriche. Le forze magnetiche sono le forze che si esercitano tra correnti elettriche.
Gli elettroni sono particelle che portano una carica elettrica negativa. Esistono altri tipi di particelle, ma gli elettroni sono responsabili della maggior parte di quel che abbiamo bisogno di conoscere sul comportamento delle onde radio.
Diamo un’occhiata a quel che succede in un pezzo di filo diritto, nel quale spingiamo gli elettroni da un capo all’altro e viceversa, periodicamente. Ad un certo momento, la cima del cavo sarà caricato negativamente – tutti gli elettroni negativi sono accumulati lì. Questo crea un campo elettrico dal positivo al negativo lungo il filo. Al momento successivo, gli elettroni sono stati tutti guidati all’altro capo, e il campo elettrico punta nell’altro senso. Dato che questo succede ancora e ancora, i vettori del campo elettrico (frecce che indicano dal positivo al negativo) lasciano il filo, e sono irradiati nello spazio attorno al filo stesso.
Quel che abbiamo appena desciritto è conosciuto anche come dipolo (il nome deriva dall’avere due poli, positivo e negativo) o, più comunemente antenna a dipolo. E’ la versione più semplice di antenna omnidirezionale. Il ![]() movimento
movimento ![]() del campo elettrico è comunemente chiamato onda elettromagnetica.
del campo elettrico è comunemente chiamato onda elettromagnetica.
Torniamo alla relazione:
Velocità = Frequenza * Lunghezza d’onda
Nel caso di onde elettromagnetiche, la velocità è quella della luce, indicata con c.
c = 300,000 km/s = 300,000,000 m/s = 3*10^8 m/s c = f * λ
Le onde elettromagnetiche, a differenza dalle onde meccaniche, non richiedono un mezzo per propagarsi. Le onde elettromagnetiche possono propagarsi anche nel vuoto.
Potenze del dieci
Nella fisica, matematica ed ingegneria, si usa esprimere i numeri come potenze del dieci. Incontreremo spesso questi termini, ad esempio nei Giga-Hertz (GHz), Centi-metri (cm), Micro-secondi (µs) e così via.
Potenze del dieci |
|||
Nano- |
10-9 |
1/1000000000 |
n |
Micro- |
10-6 |
1/1000000 |
µ |
Milli- |
10-3 |
1/1000 |
m |
Centi- |
10-2 |
1/100 |
c |
Kilo- |
103 |
1 000 |
k |
Mega- |
106 |
1 000 000 |
M |
Giga- |
109 |
1 000 000 000 |
G |
Conoscendo la velocità della luce, possiamo calcolare la lunghezza d’onda per una data frequenza. Prendiamo ad esempio la frequenza delle reti wireless 802.11b:
f = 2.4 GHz
= 2,400,000,000 cicli / secondo
Lunghezza d’onda lambda (λ) = c / f
= 3*10^8 / 2.4*10^9
= 1.25*10^-1 m
= 12.5 cmFrequenza e lunghezza d’onda determinano la maggior parte del comportamento di un’onda elettromagnetica, dall’antenna che andremo a costruire agli oggetti che sono sul percorso della rete che intendiamo realizzare. Esse sono responsabili di molte delle differerenze tra i differenti standard che potremmo scegliere. Per questo capire i concetti base di frequenza e lunghezza d’onda ci aiuterà molto nelle attività pratiche con il wireless.
Polarizzazione
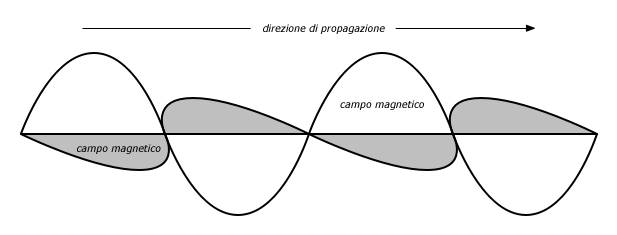
Un’altra caratteristica importante delle onde elettromagnetiche è la polarizzazione. La polarizzazione descrive la direzione del vettore del campo elettromagnetico.
Se immaginiamo un’antenna a dipolo verticale (un pezzo di filo diritto), gli elettroni si muoveranno solamente su e giù, non lateralmente (perché non c’è spazio per muoversi), così i campi elettrici punteranno solo verso il basso o verso l’altro, verticalmente. Il campo che lascia il filo ed viaggia come onda avrà una polarizzazione strettamente lineare (e, in questo caso, verticale). Se invece poniamo l’antenna a terra, orizzontalmente, avremo una polarizzazione lineare orizzontale.
|
Figura 2.2: I componenti di un’onda elettromagnetica: il campo elettrico e il campo magnetico complementare. La polarizzazione descrive l’orientamento del campo elettromagnetico. |
La polarizzazione lineare è solo un caso particolare, e non è quasi mai così perfetta: in generale, avremo sempre alcune componenti del campo che punteranno anche in altre direzioni. Il caso più generale è la polarizzazione ellittica, con polarizzazioni lineari (in una sola direzione) agli estremi e circolari (entrambe le direzioni ed uguale forza).
Come si può immaginare, la polarizzazione diventa importante nel momento in cui si allineano le antenne. Se si ignora la polarizzazione si può avere un segnale molto debole anche con le migliori antenne. In questo caso si parla di ![]() errore di polarizzazione
errore di polarizzazione ![]() .
.
Lo spettro elettromagnetico
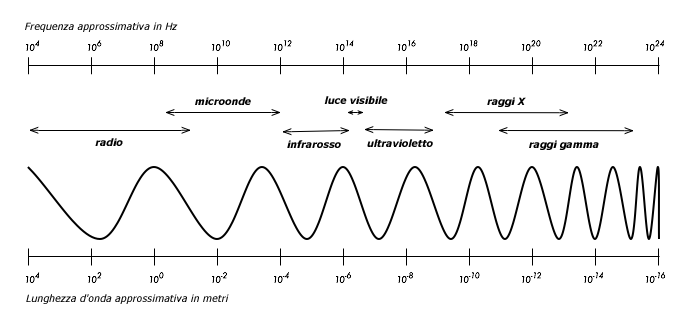
Le onde elettromagnetiche si estendono in un’ampia gamma di frequenze (e, conseguentemente, di lunghezze d’onda). Questa gamma di frequenze e lunghezze d’onda è chiamato spettro elettromagnetico. La porzione dello spettro più familiare agli uomini è probabilmente quella della luce, la parte visibile dello spettro elettromagnetico. La luce si trova all’incirca tra le frequenze di 7.5*1014 Hz e 3.8*1014 Hz, con corrispondenti lunghezze d’onda da circa 400 nm (viola/blu) a 800 nm (rosso).
Siamo regolarmente esposti anche ad altre regioni dello spettro elettromagnetico, compreso le AC (correnti alternate) o corrente di rete, a 50/60 Hz, raggi-X / radiazioni Roentgen, ultravioletti (appena sopra il confine della luce visibile), infrarosso (frequenze immediatamente inferiori a quelle della luce visibile) e molte altre. Radio è il termine usato per la porzione dello spettro elettromagnetico nel quale le onde possono essere generate applicando una corrente alternata ad un’antenna. Questo è vero per la gamma compresa tra 3 Hz e 300 GHz, ma nel senso più stretto del termine il limite massimo di frequenza sarebbe 1 GHz.
Quando si parla di radio, molte persone pensano alla radio FM, che utilizza una frequenza di circa 100 MHz. Tra la radio e l’infrarosso troviamo la porzione delle microonde, con frequenze da circa 1 GHz fino a 300 GHz e lunghezze d’onda da 30 cm ad 1 mm.
L’uso più comune delle microonde è il forno domestico, che di fatti lavora esattamente nella stessa ![]() gamma degli standard wireless con cui abbiamo a che fare. Queste frequenze si trovano all’interno della gamma per uso libero, senza bisogno di concessioni. Questa gamma di frequenze è chiamata banda ISM, dove ISM sta per Industriale, Scentifico e Medico
gamma degli standard wireless con cui abbiamo a che fare. Queste frequenze si trovano all’interno della gamma per uso libero, senza bisogno di concessioni. Questa gamma di frequenze è chiamata banda ISM, dove ISM sta per Industriale, Scentifico e Medico ![]() . La maggior parte delle altre regioni dello spettro sono strettamente regolamentate da leggi e concessioni, con licenze dal notevole aspetto economico soprattutto per quelle porzioni dello spettro utilizzabili per trasmissioni radio e TV o per comunicazione di voce e dati. In molti paesi le bande ISM sono invece state riservate per uso senza necessità di licenze.
. La maggior parte delle altre regioni dello spettro sono strettamente regolamentate da leggi e concessioni, con licenze dal notevole aspetto economico soprattutto per quelle porzioni dello spettro utilizzabili per trasmissioni radio e TV o per comunicazione di voce e dati. In molti paesi le bande ISM sono invece state riservate per uso senza necessità di licenze.
|
Figura 2.3: Lo spettro elettromagnetico. |
Le frequenze per noi più interessanti sono quelle comprese tra 2.412 - 2.484 GHz, utilizzate dagli standard radio 802.11b e 802.11g (corrispondenti alle lunghezze d’onda di circa 12.5 cm). Altre apparecchiature comunemente disponibili utilizzano lo standard 802.11a che opera nei 5.170 - 5.805 GHz (corrispondenti alle lunghezze d’onda da 5 a 6 cm circa).
Larghezza di banda
Un termine che incontreremo spesso nella fisica delle onde radio è la larghezza di banda. E’ semplicemente una misura dell’ampiezza della gamma di frequenze. Se un dispositivo utilizza una gamma da 2.40 GHz a 2.48 GHz allora la larghezza di banda sarà di 0.08 GHz (o, più semplicemente, 80MHZ).
E’ semplice notare che la larghezza di banda che stiamo definendo è in stretto rapporto con la quantità di dati che possiamo trasmetterci sopra; più “spazio” c’è tra le frequenze, maggiore sarà la quantità di dati che potremo farci entrare in un certo tempo. Il termine larghezza di banda è usato spesso per qualcosa che invece dovremmo chiamare velocità di trasferimento dati (data rate), cosicchè con “la mia connessione a Internet ha una larghezza di banda di 1 Mbps” intendiamo che può trasmettere dati a 1 megabit al secondo.
Frequenze e canali
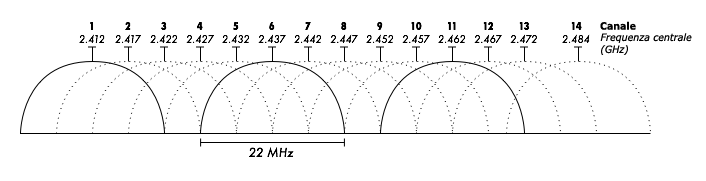
Diamo un’occhiata un pò più da vicino al come viene utilizzata la banda 2.4 GHz nel 802.11b. Lo spettro è suddiviso porzioni di eguale dimensione e uniformemente distribuiti come canali. Notiamo come i canali sono “larghi” 22 MHz e sono separati da solo 5 MHz. Ciò significa che i canali adiacenti si sovrappongono, e possono interferire l’uno con l’altro. Nella Figura 2.4 è rappresentata visualmente questa suddivisione.
|
Figura 2.4: Canali e frequenze centrali dello 802.11b. Notiamo che i canali 1, 6, e 11 non si sovrappongono. |
Per la lista completa dei canali e delle loro frequenze centrali negli standard 802.11b/g e 802.11a, vedere l’Appendice A.
Comportamento delle onde radio
Ci sono alcune semplici regole che possono rivelarsi estremamente utili quando si inizia a progettare una rete wireless:
- Maggiore è la lunghezza d’onda, più lontano arriverà il segnale
- Maggiore è la lunghezza d’onda, meglio il segnale viaggerà attorno ed attraverso gli ostacoli
- Minore è la lunghezza d’onda, maggiore è la quantità di dati che potrà trasportare
Tutte queste regole, per quanto semplici possano essere, sono comprensibili ancor meglio con qualche esempio.
Le onde più lunghe arrivano più lontano
A parità di potenza, le onde con una maggiore lunghezza tendono ad arrivare più lontano rispetto alle onde più corte. Questo effetto è visibile spesso con le radio FM, comparando la portata di un trasmettitore FM a 88 MHz con uno a 108MHz. I trasmettitori con frequenza minore tendono a raggiungere distanze più elevate rispetto ai trasmettitori in alta frequenza alla stessa potenza.
Le onde più lunghe passano attorno agli ostacoli
Un’onda sull’acqua lunga 5 metri non verrà fermata da un pezzetto di legno da 5 mm che vi galleggia dentro. Se invece il pezzo di legno fosse grande 50 metri (ad esempio una nave), ![]() it would be well in the way of the wave
it would be well in the way of the wave ![]() . La distanza che un’onda può coprire dipende dalla relazione tra la sua lunghezza d’onda e la dimensione degli ostacoli sul suo percorso di propagazione.
. La distanza che un’onda può coprire dipende dalla relazione tra la sua lunghezza d’onda e la dimensione degli ostacoli sul suo percorso di propagazione.
E’ difficile immaginarsi onde che si muovono attraverso oggetti solidi, ma questo è il caso delle onde elettromagnetiche. Onde più lunghe (e quindi frequenze più basse) tendono a penetrare meglio gli oggetti rispetto alle onde più corte (e quindi a frequenza più alta). Ad esempio, il segnale radio FM (88-108 MHz) può viaggiare attraverso palazzi e altri ostacoli facilmente mentre onde più corte (come ad esempio il segnale telefonico GSM operante a 900 o 1800 MHz) fanno più fatica. Questa differenza è dovuta in parte alla differenza in termini di potenza utilizzata per FM e GSM, ma è in parte anche dovuta alla minore lunghezza d’onda del segnale GSM.
Le onde più corte possono trasportare più dati
Più velocemente pulsano le onde, maggiore è la quantità di dati che possono trasportare: ogni ciclo potrebbe essere utilizzato per trasportare ad esempio un bit digitale, uno ‘0’ o un ‘1’, un ‘si’ o un ‘no’. C’è un altro principio che può essere applicato ad ogni tipo di onda e che è estremamente utile per comprendere la propagazione delle onde radio. Si tratta del principio conosciuto come il principio di Huygens, da Christiaan Huygens, matematico, fisico e astronomo olandese (1629 – 1695).
Immaginiamo di prendere un bastoncino e lasciarlo cadere verticalmente sulla superfice calma di un lago facendo oscillare e danzare l’acqua. Le onde si allontaneranno dal centro del bastone in modo circolare. Ora, ovunque stiano ballando le particelle di acqua, faranno in modo che le particelle circostanti si comportino allo stesso modo: ![]() una nuova onda circolare partirà da ogni punto di dispersione
una nuova onda circolare partirà da ogni punto di dispersione ![]() . Questo è in parole semplici il principio di Huygens. Secondo la definizione di http://wikipedia.org/ :
. Questo è in parole semplici il principio di Huygens. Secondo la definizione di http://wikipedia.org/ :
“Il principio di Huygens è un metodo di analisi applicato ai problemi della propagazione delle onde alle estremità remote del campo. In esso si riconosce che ogni punto di avanzamento del fronte dell’onda è infatti il centro di una nuova dispersione e la sorgente di un nuovo treno di onde, e che l’avanzare dell’onda intera può essere vista come la somma delle onde secondarie
 che provengono da punti già attraversati del mezzo di propagazione
che provengono da punti già attraversati del mezzo di propagazione  . Questa visuale della propagazione delle onde aiuta a comprendere meglio la varietà dei fenomeni delle onde, come la diffrazione.”
. Questa visuale della propagazione delle onde aiuta a comprendere meglio la varietà dei fenomeni delle onde, come la diffrazione.”
Questo principio risulta vero sia per le onde radio che per quelle sull’acqua, per il suono e per la luce. Per la luce le lunghezze d’onda sono troppo piccole affinchè un uomo possa osservarne gli effetti direttamente. Il principio ci aiuta a capire sia il fenomeno della diffrazione che quello degli ![]() anelli di Fresnel, the need for line of sight as well as the fact that sometimes we seem to be able to go around corners, with no line of sight.
anelli di Fresnel, the need for line of sight as well as the fact that sometimes we seem to be able to go around corners, with no line of sight. ![]()
Diamo ora uno sguardo a quel che accade alle onde elettromagnetiche durante il loro cammino.
Assorbimento
Quando attraversano qualcosa (qualche materiale), le onde elettromagnetiche subiscono un indebolimento o attenuazione. Quanto perdono in potenza dipenderà dalla loro frequenza e, ovviamente, dal tipo di materiale attraversato. Il vetro chiaro è ovviamente trasparente alla luce mentre il vetro utilizzato negli occhiali da sole porta via una parte dell’intensità luminosa e delle radiazioni ultraviolette.
Spesso un coefficiente di assorbimento è utilizzato per descrivere l’impatto di un materiale sulle radiazioni. Per le microonde i due materiali assorbenti principali sono:
Metalli. Gli elettroni possono muoversi e oscillare liberamente nei metalli e per questo sono capaci di assorbire l’energia di un’onda in transito.
Acqua. Le microonde riescono ad agitare le molecole di acqua che così portano via parte dell’energia delle onde stesse.
Per gli scopi pratici del wireless networking, possiamo considerare i metalli e l’acqua come assorbenti perfetti, non saremo in grado di attraversarli (sebbene strati sottili di acqua permettono il passaggio di piccole potenze). Per le microonde questi materiali sono come una parete di mattoni per la luce. Quando parliamo di acqua dobbiamo ricordare che è possibile incontrarla in forme diverse: pioggia, nebbia, foschia, nuvole basse e così via, tutto può frapporsi ad un collegamento radio. Questi fattori hanno una grossa influenza e, in molti casi, un mutamento meteorologico può interrompere un collegamento radio.
Ci sono altri materiali, inoltre, che hanno un effetto più complesso sull’assorbimento radio.
Per gli alberi e il legno, la quantità di assorbimento dipenderà dalla quantità di acqua che contengono. Il legno vecchio e secco è più o meno trasparente, il legno fresco e umido assorbirà molto.
Le plastiche e i materiali simili generalmente non assorbono molta energia radio, il loro assorbimento dipenderà dalla frequenza e dal tipo di materiali. Prima di costruire un componente in plastica (ad esempio una protezione contro il tempo per un dispositivo radio e la sua antenna), è sempre una buona idea misurare e verificare che il materiale usato non assorba energia ad una frequenza di 2.4 GHz. Un metodo semplice per misurare l’assorbimento di una plastica a 2.4 GHz è metterne un pezzo in un forno a microonde per un paio di minuti. Se la plastica si riscalda, allora assorbe energia radio e non dovrebbe essere utilizzato per coprire i nostri dispositivi.
Infine parliamo di noi: gli esseri umani (così come gli altri animali) sono largamente composti di acqua e, chiedendolo ad un’onda radio, potremmo essere descritti come delle grandi sacche d’acqua, con lo stesso grande assorbimento. Orientare un access point di un ufficio in modo che il segnale deppa oltrepassare molte persone è un grosso errore che si può commettere nella costruzione di una rete. Lo stesso si può dire per gli hotspots, nei bar, nei locali, librerie e installazioni all’aperto.
Riflessione
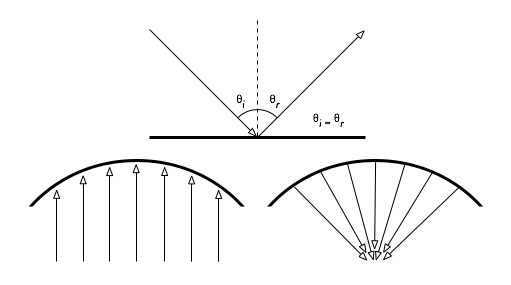
Esattamente come la luce visibile, le onde radio sono riflesse quando vengono in contatto con materiali adatti a farlo: i metalli e le superfici d’acqua sono i principali riflettenti per le onde radio. Le regole per la riflessione sono abbastanza semplici: l’angolo con cui un’onda colpisce la superfice è lo stesso angolo con cui essa verrà riflessa. Notiamo che per un’onda radio, una griglia densa ha lo stesso effetto di una superfice solida, fin quando la distanza tra le barre della griglia è più piccola della lunghezza d’onda. A 2.4 GHz una griglia metallica da un centimetro si comporterà come una lastra di metallo.
|
Figura 2.5: Riflessione delle onde radio. L’angolo di incidenza è sempre uguale all’angolo di riflessione. |
Nella parabola questo effetto è utilizzato per concentrare in una direzione comune le onde radio che ne colpiscono la superfice. Anche se le regole della riflessione sono abbastanza semplici, le cose possono complicarsi quando immaginiamo l’interno di un ufficio con molti piccoli oggetti di metallo di svariate forme diverse. Lo stesso si può dire degli ambienti urbani. Questo spiega perché gli effetti di ![]() eco (multipath effect)
eco (multipath effect) ![]() (segnali che raggiungono lo stesso punto seguendo percorsi diversi e quindi in tempi diversi) giocano un ruolo così importante nel wireless networking. Le superfici d’acqua, con le loro onde e increspature che cambiano continuamente, costituiscono un oggetto riflettente estremamente complicato tanto che è più o meno impossibile calcolare e predirne gli effetti.
(segnali che raggiungono lo stesso punto seguendo percorsi diversi e quindi in tempi diversi) giocano un ruolo così importante nel wireless networking. Le superfici d’acqua, con le loro onde e increspature che cambiano continuamente, costituiscono un oggetto riflettente estremamente complicato tanto che è più o meno impossibile calcolare e predirne gli effetti.
Dovremmo aggiungere che anche la polarizzazione ha un impatto: onde polarizzate diversamente vengono in genere riflesse diversamente.
Nella costruzione di antenne utilizziamo la riflessione a nostro vantaggio, ad esempio ponendo delle grandi parabole dietro i trasmettitori/ricevitori per raccogliere e concentrare i segnali radio in un piccolo punto.
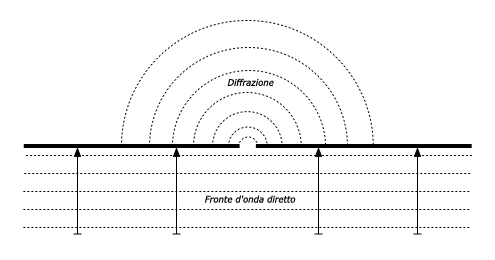
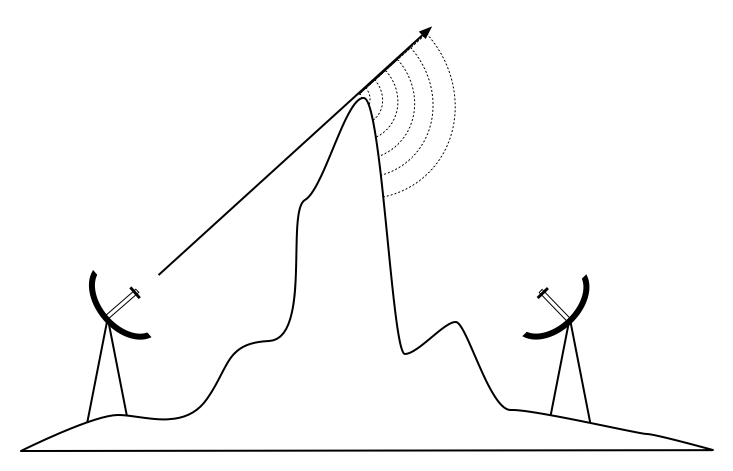
Diffrazione
La diffrazione è l’apparente piegarsi delle onde quando colpiscono un oggetto. E’ l’effetto delle “onde intorno agli angoli”. Immaginiamo un’onda sull’acqua che viaggia con un fronte diritto, ![]() esattamente come un’onda che vediamo avanzare su una spiaggia d’oceano. Ora mettiamo un ostacolo solido, diciamo una buona barriera di legno, sul suo cammino per fermarla. Ora ritagliamo una stretta fessura in questa barriera. Appena l’apriremo, un’onda circolare partirà e ovviamente raggiungerà punti che non sono esattamente in linea dietro questa fessura ma neanche davanti. Se guardiamo questo fronte d’onda (potrebbe essere anche un’onda elettromagnetica) potrà risultare difficile spiegarsi come esso possa raggiungere punti che dovrebbero essere nascosti dalla barriera. Ma quando prende la forma di un fronte d’onda, il fenomeno
esattamente come un’onda che vediamo avanzare su una spiaggia d’oceano. Ora mettiamo un ostacolo solido, diciamo una buona barriera di legno, sul suo cammino per fermarla. Ora ritagliamo una stretta fessura in questa barriera. Appena l’apriremo, un’onda circolare partirà e ovviamente raggiungerà punti che non sono esattamente in linea dietro questa fessura ma neanche davanti. Se guardiamo questo fronte d’onda (potrebbe essere anche un’onda elettromagnetica) potrà risultare difficile spiegarsi come esso possa raggiungere punti che dovrebbero essere nascosti dalla barriera. Ma quando prende la forma di un fronte d’onda, il fenomeno ![]()
|
Figura 2.6: Diffrazione attraverso una stretta fessura. |
Il principio di Huygens fornisce un modello per comprendere questo comportamento. Immaginiamo che, ad un certo istante, ogni punto di un ![]() fronte d’onda
fronte d’onda ![]() può essere considerato il punto di origine di un’onda sferica
può essere considerato il punto di origine di un’onda sferica ![]() (wavelet)/!\ . Questa idea è stata poi sviluppata da Fresnel e anche se descrive adeguatamente il fenomeno, è ancora fonte di dibattito. Per i nostri scopi il modello di Huygens descrive l’effetto più che bene.
(wavelet)/!\ . Questa idea è stata poi sviluppata da Fresnel e anche se descrive adeguatamente il fenomeno, è ancora fonte di dibattito. Per i nostri scopi il modello di Huygens descrive l’effetto più che bene.
|
Figura 2.7: Il principio di Huygens. |
Come effetto della diffrazione, le onde “curveranno” attorno agli angoli o tramite aperture negli ostacoli. Le lunghezze d’onda della luce visibile sono troppo piccole affinchè un uomo possa osservare questo effetto direttamente. Le microonde, con una lunghezza d’onda di diversi centimetri, mostrano questo l’effetto della diffrazione quando le onde colpiscono muri, vette di montagne e altri ostacoli.
|
Figura 2.8: Diffrazione sulla cima di una montagna. |
Notiamo come la diffrazione arrivi a scapito della potenza: l’energia dell’onda diffratta è significantemente minore di quella del fronte d’onda che l’ha originata. Ma, in alcune applicazioni specifiche, possiamo trarre vantaggio dall’effetto della diffrazione per aggirare gli ostacoli.
Interferenza
Quando si lavora con le onde, uno più uno non da necessariamente due. Potrebbe anche dare zero.
|
Figura 2.9: Interferenza |
Si può intuire facilmente disegnando due onde sinusoidali e sommandone le ampiezze. Quando un picco si somma all’altro picco, potremmo avere il massimo risultato (1 + 1 = 2). Chiameremo questo caso interferenza costruttiva. Quando un picco si somma ad una “valle”, avremmo il completo annientamento ((1 + (-)1 = 0), saremo in presenza di interferenza distruttiva.
Possiamo fare una prova nell’acqua usando due piccoli bastoncini per creare delle onde circolari, vedremo che dove le onde si incrociano, ci saranno aree con picchi più alti ed altre dove l’acqua rimarrà piatta e calma.
Per far si che interi treni d’onda si sommino o si cancellino perfettamente a vicenda, essi dovrebbero avere la stessa esatta lunghezza d’onda e una relazione fissa di fase, che corrisponde ad una posizione fissa dei picchi di un’onda rispetto all’altra.
Nella tecnologia wireless, la parola interferenza è usata tipicamente in un senso più ampio, per descrivere il disturbo proveniente da altre sorgenti RF come i canali vicini. Quandi quando gli esperti di wireless networking parlano di interferenze, intendono tipicamente tutti i tipi di disturbi che possono provenire sia da altre reti che da altre sorgenti di microonde. L’interferenza è una delle fonti maggiori di difficoltà nella costruzione di collegamenti wireless, specialmente negli ambienti urbani o negli spazi chiusi (come una sala conferenze) dove diverse reti possono accaparrarsi l’uso dello spettro di frequenze.
Ogni volta che onde di eguale ampiezza e fase opposta incrociano il loro cammino, si annullano e nessun segnale potrà essere ricevuto. La causa più comune è che le onde si combinano per formare un’onda distorta che non può essere usata efficientemente per le comunicazioni. Le tecniche di modulazione e l’utilizzo canali multipli aiuta ad affrontare il problema delle interferenze, ma non riesce ad eliminarlo completamente.
/!\ Line of sight /!\
Il termine ![]() line of sight
line of sight ![]() è abbastanza semplice da comprendere quando si parla di luce visibile: se possiamo vedere un punto B da un punto A i due punti sono sulla stessa traiettoria visiva. Tracciamo una linea da A a B e se non c’è nulla nel mezzo, avremo una
è abbastanza semplice da comprendere quando si parla di luce visibile: se possiamo vedere un punto B da un punto A i due punti sono sulla stessa traiettoria visiva. Tracciamo una linea da A a B e se non c’è nulla nel mezzo, avremo una ![]() line of sight
line of sight ![]() .
.
Le cose si complicano leggermente quando abbiamo a che fare con le microonde. Ricordiamoci che la maggior parte delle caratteristiche di propagazione delle onde elettromagnetiche scalano con la loro lunghezza d’onda. E’ il caso anche dell’allargarsi delle onde durante il loro viaggio. La luce ha una lunghezza d’onda di circa 0.5 micrometri, le microonde utilizzate nel wireless networking hanno una lunghezza d’onda di pochi centimetri. Conseguentemente i loro ![]() fronti
fronti ![]() sono molto più larghi, possiamo dire che necessitano di più spazio.
sono molto più larghi, possiamo dire che necessitano di più spazio.
Notiamo che i fronti dellla luce visibile hanno la stessa larghezza e, se li lasciamo viaggare abbastanza a lungo, potremmo vedere i risultati nonostandte la loro corta lunghezza d’onda. Puntando un laser bene a fuoco verso la luna, il suo fascio si allargherà fino a oltre 100 metri di raggio prima di raggiungere la superfice. Possiamo osservare direttamente questo effetto utilizzando un puntatore laser economico ed un binocolo in una notte serena. Invece che puntare alla luna, punteremo a una montagna distante o a una struttura abbandonata (ad esempio una ciminiera). Il raggio del fascio luminoso aumenterà proporzionalmente alla distanza.
La ![]() linea di vista
linea di vista ![]() di cui abbiamo bisogno per avere una connessione wireless ottimale tra due punti A e B è più di una sottile linea, dovrà avere la forma di un sigaro, un ellisse. La sua larghezza può essere descritta dal concetto degli
di cui abbiamo bisogno per avere una connessione wireless ottimale tra due punti A e B è più di una sottile linea, dovrà avere la forma di un sigaro, un ellisse. La sua larghezza può essere descritta dal concetto degli ![]() anelli di Fresnel (Fresnel zones)
anelli di Fresnel (Fresnel zones) ![]() .
.
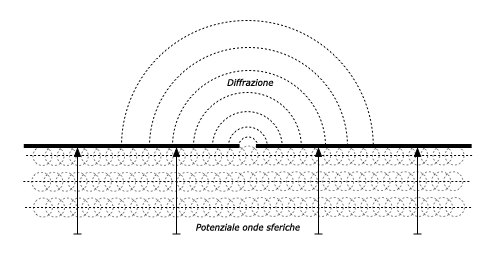
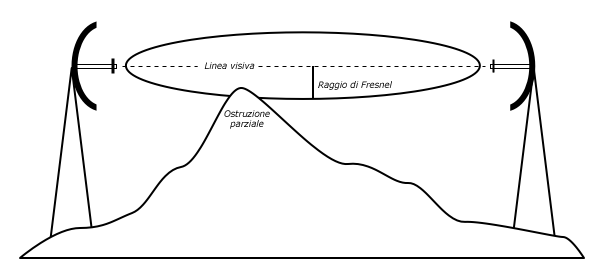
Comprendere gli anelli di Fresnel
La teoria esatta degli anelli di Fresnel è abbastanza complicata. Ad ogni modo il concetto è abbastanza semplice da comprendere: conosciamo dal principio di Huygens che una nuova onda circolare parte da ogni punto di un ![]() fronte
fronte ![]() d’onda. Sappiamo che i fasci di microonde si allargano. Sappiamo che le onde di una certa frequenza possono interferire l’una con l’altra. La teoria degli anelli di Fresnel guarda alla linea da A a B e allo spazio intorno alla linea che contribuisce a quel che arriva al punto B. Alcune onde viaggiano direttamente da A a B, mentre altre viaggiano su percorsi fuori asse. Conseguentemente, il loro percorso sarà più lungo e introdurrà una differenza di fase tra il fascio diretto e quello indiretto. Ogni volta che la differenza di fase sarà di un'intera onda otterremo un'interferenza costruttiva: i segnali si sommeranno perfettamente. Tenendo presente questo principio e facendo gli opportuni calcoli, scopriamo l'esistenza di zone ad anelli attorno all'asse tra A e B che contribuiscono al segnale che giunge al punto b.
d’onda. Sappiamo che i fasci di microonde si allargano. Sappiamo che le onde di una certa frequenza possono interferire l’una con l’altra. La teoria degli anelli di Fresnel guarda alla linea da A a B e allo spazio intorno alla linea che contribuisce a quel che arriva al punto B. Alcune onde viaggiano direttamente da A a B, mentre altre viaggiano su percorsi fuori asse. Conseguentemente, il loro percorso sarà più lungo e introdurrà una differenza di fase tra il fascio diretto e quello indiretto. Ogni volta che la differenza di fase sarà di un'intera onda otterremo un'interferenza costruttiva: i segnali si sommeranno perfettamente. Tenendo presente questo principio e facendo gli opportuni calcoli, scopriamo l'esistenza di zone ad anelli attorno all'asse tra A e B che contribuiscono al segnale che giunge al punto b.
|
Figura 2.10: La zona di Fresnel è parzialmente bloccata su questo percorso, anche se la traiettoria diretta è libera. |
E' da notare che ci sono molte possibili zone di Fresnel, noi siamo principalmente interessati alla zona 1. Se quest'area è ostacolata, ad esempio da un albero o un palazzo, il segnale che arriva a destinazione sarà attenuato. Quando costruiamo collegamenti wireless, dobbiamo assicurarci che queste zone siano libere da ostacoli. Naturalmente nulla è sempre perfetto, quindi per le applicazioni di wireless networking, dovremmo controllare che l'area che contiene il 60 percento della prima zona di Fresnel sia libera.
Ecco una formula per calcolare la prima zona di Fresnel:
r = 17.31 * sqrt(N(d1*d2)/(f*d))
...dove r è il raggio della zona in metri, N è la zona da calcolare, d1 e d2 sono le distanze tra l'ostacolo e i punti estremi del collegamento in metri, d è la lunghezza totale del collegamento in metri, e f è la frequenza in MHz. Come risultato avremo il raggio della zona di Fresnel. Per calcolare l'altezza da terra dobbiamo sottrarre questo risultato all'altezza della linea tracciata direttamente tra le sommità delle due torri.
Calcoliamo, ad esempio, la dimensione della prima zona di Fresnel al centro di un collegamento di 2 Km, supponendo di trasmettere a 2.437GHz (802.11b canale 6):
r = 17.31 sqrt(1 * (1000 * 1000) / (2437 * 2000)) r = 17.31 sqrt(1000000 / 4874000) r = 7.84 metri
Supponendo che entrambi le torri siano alte dieci metri, la prima zona di Fresnel si troverebbe ad appena 2.16 metri da terra al centro del collegamento. Quanto dovrebbe essere alta una struttura simile per poter lasciare libera la prima zona al 60%?
r = 17.31 sqrt(0.6 *(1000 * 1000) / (2437 * 2000)) r = 17.31 sqrt(600000 / 4874000) r = 6.07 metri
Sottraendo il risultato ai 10 metri, vediamo che una struttura alta 3.93 metri, al centro del collegamento, bloccherebbe fino al 60% della prima zona di Fresnel. Per migliorare la situazione, dovremmo posizionare le nostre antenne più in alto, o cambiare la direzione del collegamento per evitare gli ostacoli.
Potenza
Ogni onda elettromagnetica porta con se energia, o potenza - possiamo rendercene conto quando godiamo (o patiamo) il calore del sole. La potenza P risulta di importanza fondamentale per il funzionamento dei collegamenti wireless: abbiamo bisogno di una certa potenza minima per far si che un ricevitore riesca a captare un segnale.
Ci occuperemo ancora, con più dettagli, di potenza di trasmissione, perdita, guadagno e sensibilità radio nel capitolo tre. In questo capitolo discuteremo brevemente il come la potenza P è definita e misurata.
Il campo elettrico è misurato in V/m (differenza di potenziale per metro), la potenza contenuta in esso è proporzionale al quadrato del campo elettrico
P ~ E^2
In pratica, la potenza è misurata attraverso un qualche tipo di ricevitore come, ad esempio, un'antenna ed un voltimetro, un power meter, un oscilloscopio o anche una scheda radio ed un computer portatile. Misurare direttamente la potenza di un segnale significa misurare il segnale in Volt al quadrato.
Calcolare con i dB
La tecnica di gran lunga più importante utilizzata per calcolare la potenza è calcolare con i decibels (dB). Non si tratta di un'altra grandezza fisica, è solo un metodo conveniente per rendere i calcoli molto più semplici.
Il decibel è un'unità adimensionale, che definisce una relazione tra due misure di potenza. E' definita come:
dB = 10 * Log (P1 / P0)
dove P1 e P0 possono essere due valori qualsiasi che vogliamo comparare. Tipicamente, nel nostro caso, questi saranno due valori di potenza.
Perchè i decibel sono così pratici da usare? Molti fenomeni in natura avvengono con un comportamento che possiamo chiamare esponenziale. Per l'orecchio umano, ad esempio, un suono viene percepito con un volume doppio rispetto ad un altro se possiede dieci volte il suo segnale fisico.
Un altro esempio, più vicino al nostro campo di interesse, è l'assorbimento. Supponiamo che sul percorso del nostro collegamento wireless ci sia un muro, e che ogni metro di muro porti via la metà del segnale disponibile. Il risultato sarà:
0 metri = 1 (segnale pieno) 1 metro = 1/2 2 metri =1/4 3 metri =1/8 4 metri =1/16 n metri =1/2^n = 2^-n
Questo è un comportamento esponenziale.
Utilizzando il trucco di applicare i logaritmi (log), le cose diventano molto più semplici: invece di elevare un valore alla n-esima potenza, lo moltiplichiamo per n. Invece di moltiplicare i valori li addizioniamo semplicemente.
Ecco alcuni valori utilizzati comunemente che è importante ricordare:
+3 dB = il doppio della potenza -3 dB = la metà della potenza +10 dB = ordine di grandezza (10 volte la potenza) -10 dB = un decimo della potenza
Oltre i dB adimensionali, vi sono una serie di definizioni relative che fanno riferimento ad un certo valore base P0. Le più importanti per noi sono:
dBm relativo a P0 = 1 mW dBi relativo ad un'antenna isotropica ideale
Un' antenna isotropica è un'antenna ipotetiche che distribuisce potenza uniformemente in tutte le direzioni. Normalmente si usa approssimarla con un dipolo ma, in realtà, un'antenna isotropica perfetta non può essere costruita. Il modello isotropico è utile per definire il guadagno relativo in potenza delle antenne del mondo reale.
Un'altra convenzione comune (anche se meno conveniente) per esprimere la potenza è il milliwatt. Ecco alcune equivalenze tra potenze in milliwatt e dBm:
1 mW = 0 dBm 2 mW = 3 dBm 100 mW = 20 dBm 1W = 30 dBm
La fisica nel mondo reale
Non è da preoccuparsi se i concetti espressi in questo capitolo sembrano difficili. Capire come le onde radio si propagano e interagiscono con l'ambiente è un campo di studi complesso di per sé. La maggior parte delle persone trova difficile comprendere fenomeni che non possono nemmeno vedere con i propri occhi. Ma ormai abbiamo appreso che le onde radio non viaggiano seguendo un percorso dritto e prevedibile. Per costruire reti di comunicazione affidabili dobbiamo essere in grado di calcolare quanta potenza è richiesta per attraversare una certa distanza, e prevedere come le onde si muoveranno lungo il percorso.
C'è ancora molto da imparare sulle onde radio rispetto a quanto si è potuto esporre in questo capitolo per motivi di spazio. Per maggiori informazioni su questo campo in evoluzione vedi le risorse elencate nell'Appendice A. Ora che abbiamo un'idea di come le onde radio si comportano nel mondo reale, siamo pronti per utilizzarle per le nostre comunicazioni.